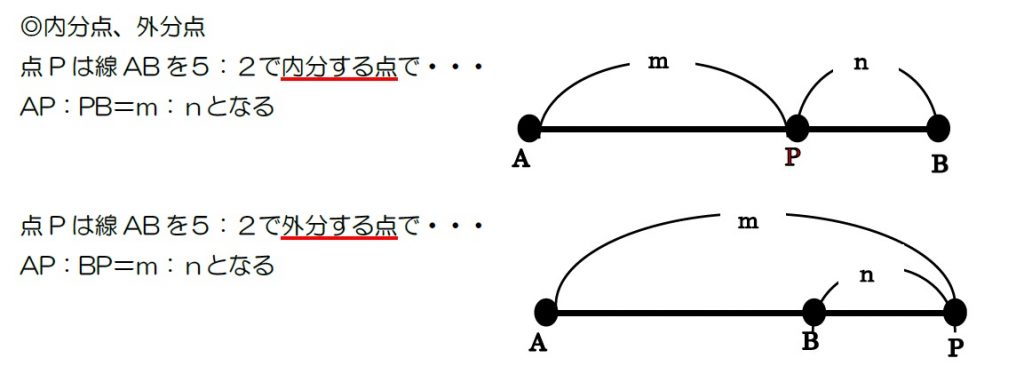
複素平面におかる内分点と外分点と重心点を求める問題です。基本的な問題です。 複素平面におかる内分点と外分点と重心点を求める問題です。基本的な問題です。 学問の問 このサイトでは、受験勉強に役立つ情報を配信していきます。特に数学の問題や解法について詳しく載せていきます外分点のとり方がイマイチ分かってないかも。内分点と外分点のとり方は上のようになります。外分点が混乱しがちですが,どちらも a → p → b という道順で進む,と理解しておくと頭の中が整理できると思います。a からスタートしたら,とにかくい09/12/19 · 内分点は全体の比を考える。 外分点は差の比を考える。 この2点が内分点、外分点を書くためには大事なポイントですね! また、外分点については2パターンの書き方がありましたね。 ここが忘れがちだし、よく質問をいただくところです。
図形と方程式の内分点外分点の問題で質問です 3 A 2b 4が Yahoo 知恵袋
内分点 外分点 座標 問題
内分点 外分点 座標 問題-高1生で習う内分点、外分点の話ですが、公式があります。しかし、それを習うのは高2のときです。じゃそれを習わないとした高1生はどう攻略していくかお話ししてい行きます。以下に例を示してお話ししていきます。 例:数直線上にa, b があります。 (1) abを3 1に内分する点pを求めよ。 (2) ab外分点の座標を求める問題です。 外分点を求める公式は、ほぼ内分点と同じでした。 小さいほうの比が負になる だけでしたね。 point abを(1)3に分ける点 2点abを13に外分する点とありますね。 外分なので 小さいほうの比をマイナス にして書き換えましょう。 abを(1)3に分ける点 を求めれば



位置ベクトルとは 内分点 外分点 三角形の重心の求め方を解説 応用問題の解き方 遊ぶ数学塾
§49 内分点と外分点 定義 実数m,n についてm≥ 0 , n≥ 0 , mn>0 とする.座標空間において, 点A とB とに対して点P が線分AB をmn に とは, ベクトル −→ AP と −→ BP とが逆の向きで,APBP=mn となることであり,m6= n のとき,R2 の点P が線分AB をmn に と は, ベクトル −→ AP と −→ BP内分と外分 ここでは直線における内分と外分について説明したいと思います。 内分 下図のように直線abがあったときに、この直線abをmnにわける点pがあったとします。このように直線abを内側で2つにわける点pのことを、直線abの内分点14/07/ · ①内分点、外分点の座標 ②点対称 ③重心の座標 2次元なので、x座標、y座標それぞれで、同じことをするだけなんです。
内分点・外分点(外分点)(数学の問題が出題されるので、解答を記入してokボタンを押してください。) さて、2点( ,0)と( ,0)を : の比に外分する点は( ,0)である。 数学を学習する 内分点 点と直線の距離の公式 三角形の面積 英語学習リンク集toeic、toefl、実用英語技能検定110 演習問題 ~ 直線 次 111 内積 上 1 ベクトルと図形 前 19 における直線の方程式 1 10 演習問題 ~ 直線 問 1 43 (内分点) 次の内分点,外分点を求めよ. (1) の 2 点 , を に内分する点. (2) の 2 点 , を に内分する点.問題編線分の内分点と外分点 問1 次の線分abを32に内分する点を図で示しましょう。 →答え 考え方比の合計と線分の距離が異なるときは、線分の距離に合わせた比の表し方にします。 比の合計は32より32=5、線分abの距離は10、32を2倍して64からapの距離は6、pbの距離は4となります
三角形の3辺の大小関係 例題 練習問題 平行線と線分比 例題 練習問題 線分の内分点と外分点 例題 練習問題 線分の比と三角形の角の二等分線 例題 練習問題 面積と比 例題 練習問題 メネラウスの定理 例題 練習問題 チェバの定理 例題 練習問題内分点・外分点の位置ベクトル 内分点 線分abをmnの比に分ける(内分する)点pの位置ベクトルは、次の式で表される。 とすると 外分点 線分abをmnの比に分ける(外分する)点pの位置ベクトルは、次の式で表される。 とすると 問 左の図のように、 oabにおいて、辺oaを32の比に内分する点をc、16/12/12 · 数学 内分点と外分点を図示する問題です。 数直線上で、abの長さは6です。 問題では、abを2:1に内分する点pを図示します。ab=6なので、ap:pb=4:2になるように点pを図示しまし


内分点と外分点の求め方 思考力を鍛える数学



高校数学 数a 勉強動画 内分 外分 の問題 19ch
複素数の内分点・外分点 複素数平面における内分点,外分点の基本公式と図形的な位置を確かめる教材です.教科書レベルの問題です.演習問題は画面上で採点できます. 2直線の交点 複素数の1次独立を使って複素数平面における2直線の交点を求める問題と解説です.演習問題は画面上で内分点,外分点の作図は,線分の作図の基本となるものなので,確実にマスターしておきましょう。 また,作図は,慣れることも必要ですので,様々な問題にチャレンジしていきましょうね。 これで回答を終わります。ご理解いただけましたか? これから今回は数直線上の内分点と外分点の位置について解説していきます。線分の並びと内分外分の順番に注意して解いていきましょう。 教科書より詳しい高校数学 高校数学Ⅰ 数と式 集合と論理 2次関数 図形と計量 データの分析 高校数学A 場合の数と確率 整数の性質 図形の性質 高校数学



基本 平面上での内分点と外分点 なかけんの数学ノート


Studydoctor 数a 内分点と外分点の作図 描き方 Studydoctor
06/03/21 · 内分点,外分点の公式はよく使うので丸暗記をオススメしますが,このように一瞬で導出できるので忘れても問題ありません。 同じ公式が四回も(座標,平面ベクトル,空間ベクトル,複素数平面)登場することで教科書の紙面を圧迫しています。 数学2内分点・外分点 2 解説 内分点 の 《問題》 以下の問題 において,分母の空欄が2つあるところは,公式の順に数値を入れるものとします.(タブキーで空欄の移動ができます.) (1) 2点A(3),B(7)を結ぶ線分ABを2:1に内分する点Pの座標pは ×3+ ×7 p = + = (2) 2点A(2),B(5)を内分点・外分点(内分点)(数学の問題が出題されるので、解答を記入してok ボタンを押してください。) さて、2点( ,0)と( ,0)を : の比に内分する点は( ,0)である。 外分点 数学を学習する 余弦定理 ベクトルの内積 三角形の面積 英単語のれんしゅう英単語練習のための



内分点 外分点の公式と求め方 数直線 座標 ベクトル 複素数



4プロセス66 三点が一直線上にある 高校数学に関する質問 勉強質問サイト
「問題」の記事一覧です。 「問題」の記事一覧です。 0801内分点と外分点を求める(難易度1) 19/7/11 問題 0901内分点とベクトルがなす角を求める(難易度2) 19/7/12 問題 1001ベクトルの方程式から点の位置を求める(難易度3) 19/7/11 問題 First;内分点,外分点の作図は,線分の作図の基本となるものなので,確実にマスターしておきましょう。 また,作図は,慣れることも必要ですので,様々な問題にチャレンジしていきましょうね。 これで回答を終わります。ご理解いただけましたか? これから内分点については,「 11 に内分する」点というものがあります.( ab の真ん中の点中点というがそうです.)これに対して,外分点については,同じ比率すなわち「 11 に外分する」点というものはありません. 次の図から分かるように,一方の端を月まで伸ばしても, ab の分だけ大きい方



2点間の距離 内分 外分する点の座標の求め方 数学の偏差値を上げて合格を目指す



位置ベクトルを超わかりやすく解説した 内分 外分 重心 理系ラボ
内分点 1013 3.外分点 928 補.線分と外分点の位置関係 249 4.xy平面上に図形をかく 302 5.2点間の距離 508 6.xy平面上の内分点・外分点 919内分点と外分点の計算問題 点A(-1、-5)と点B(3、4)を1:2に内分する点Pと、3:1に外分する点Qの座標を求めてみましょう。 内分点 座標上の2点間の内分点を求める公式は覚えていますか? 点A(x1,y1)と点B(x2,y2)をm:nに内内分点・外分点の問題 みなさん、こん は。本ブログを見ていただいてありがとうございます。 では問題を解いてみましょう。 今日の問題はこちら。 続きを読む yuji_nakano 2249 広告を非表示にする もっと読む;



内分点 外分点の位置ベクトル 数学b フリー教材開発コミュニティ Ftext



位置ベクトルの意味と内分点 外分点の位置ベクトルの考え方 アタリマエ
複素数平面上での内分点、外分点の公式です。 1. $z_1=15i,~z_2=32i$を表す点をA, Bとするとき,ABを$21$の比に内分およびメネラウスの定理では外分点が必ず登場します。 例題2 abcの辺abを31に外分する点をp、辺acを81に外分する点をrとする。 直線prと直線bcの交点をqとするとき、bccqを求めなさい。 ポイント 外分点の取り方は大丈夫でしょうか? 例題2の解答内分点・外分点や重心の問題なども解説していきますので、この記事を通してぜひマスターしてくださいね。 目次 位置ベクトルとは? 位置ベクトルの公式 公式①2 点を結ぶベクトルと位置ベクトル 公式②内分点の位置ベクトル 公式③外分点の位置ベクトル 公式④三角形の


位置ベクトル の考え方 内分点 外分点の位置ベクトル
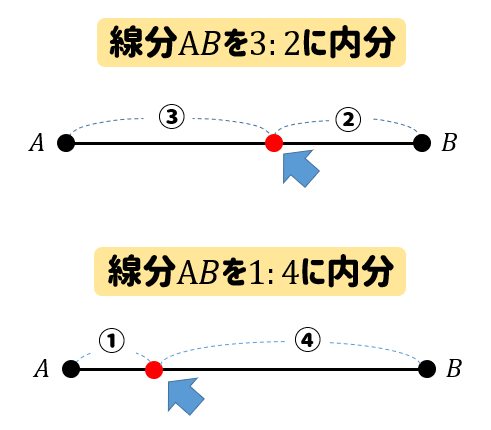


数学a 内分 外分の点はどこにある 場所の見つけ方をサクッと解説 数スタ
Try IT(トライイット)の線分ABを mnに内分する点Pの例題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。09/06/ · から内分・外分点の座標を求めることを考えます。私たちに与えられるのは座標と比だけであることが多いですからね。 内分点の座標公式 まずは内分から考えていきましょう。内分する点Pの座標を \(P(p)\) とおきます。そうすると例えば次のような時れる。ここの話を突き詰めても前進しないので,ここでは問題提起にとどめておくことにする。 生徒に対しては誤解を招かぬ様,合計の様なもの,と表現するようにしている。 3 図的表現へのアプローチ 例1 を図示することを考えよう。 図1 の様に表現できる。これは2 3 の内分を表すこ 40


図形と方程式の内分点外分点の問題で質問です 3 A 2b 4が Yahoo 知恵袋



数bの問題の解説をお願いします Okwave


数学a 内分点と外分点の作図のやり方とコツ ページ 2 教科書より詳しい高校数学


街角の数学 Street Wasan
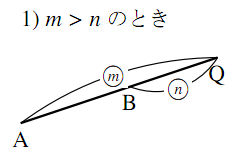


内分と外分 数学a フリー教材開発コミュニティ Ftext
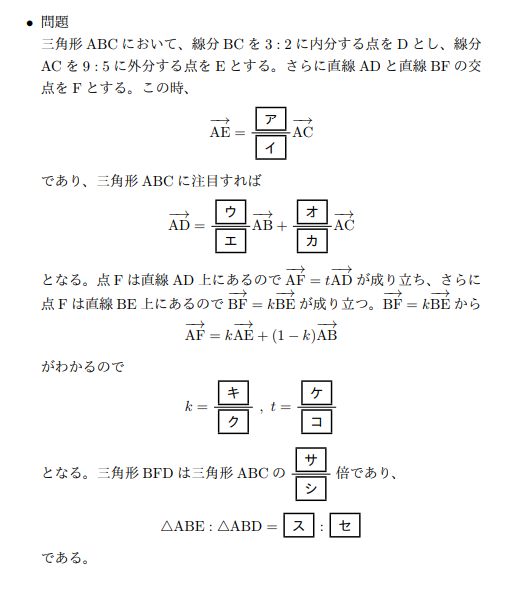


必ず押さえておきたいベクトルの問題その2 Part1 高校数学の知識庫


ベクトルの内分 外分



6講 座標空間における図形 問題集 2章 空間のベクトル



位置ベクトルの意味と内分点 外分点の位置ベクトルの考え方 アタリマエ
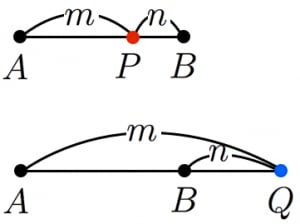


内分点 外分点の公式と証明 高校数学の美しい物語



内分点 外分点 重心 高校数学 図形と方程式 4 Youtube



赤線のところはなぜこのようになるのですか Clear



数学 複素数平面 Ppt Download



位置ベクトルとは 公式 内分 外分 重心 や求め方 練習問題 受験辞典
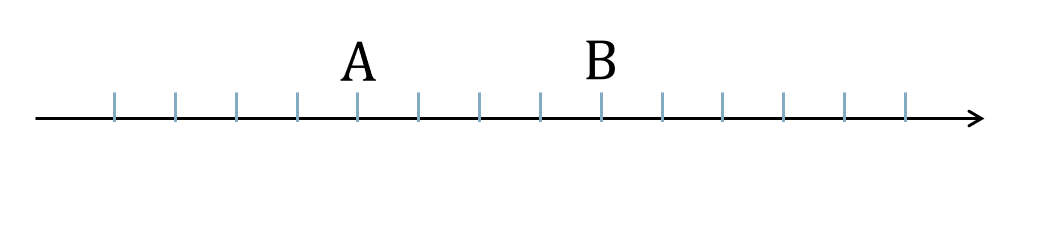


数学a 内分点と外分点の位置の求め方とコツ 教科書より詳しい高校数学



直線上における内分点と外分点 数学ii By Okボーイ マナペディア
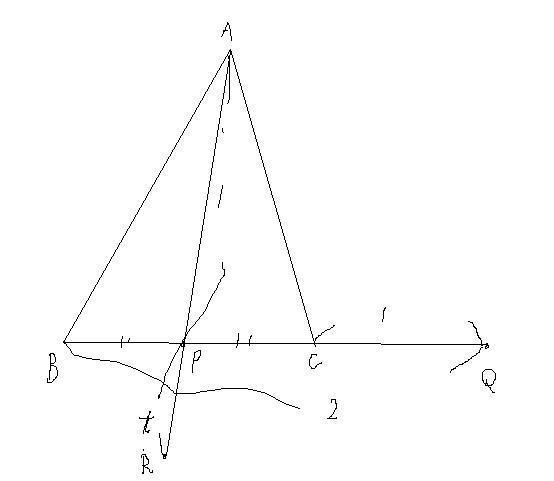


内分点 外分点のベクトル 三角形の面積比の問題です 大学入試数学問題の解説 解答
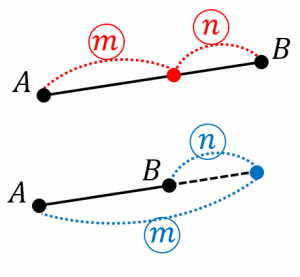


内分点と外分点の座標を求める公式 具体例で学ぶ数学


高校数学 問題検索 数学 図形と方程式 内分点 外分点 平行四辺形 重心 数学



外分する点をdとするとき Vecoc ア Baroa Dfracsquar クァンダ Qanda で解き方を見る



位置ベクトルとは 内分点 外分点 三角形の重心の求め方を解説 応用問題の解き方 遊ぶ数学塾


内分点と外分点の求め方 思考力を鍛える数学



内分点 外分点のベクトル 三角形の面積比の問題です 大学入試数学問題の解説 解答



1講 位置ベクトル 2節 ベクトルと平面図形 問題集 1章 平面上のベクトル



外分点
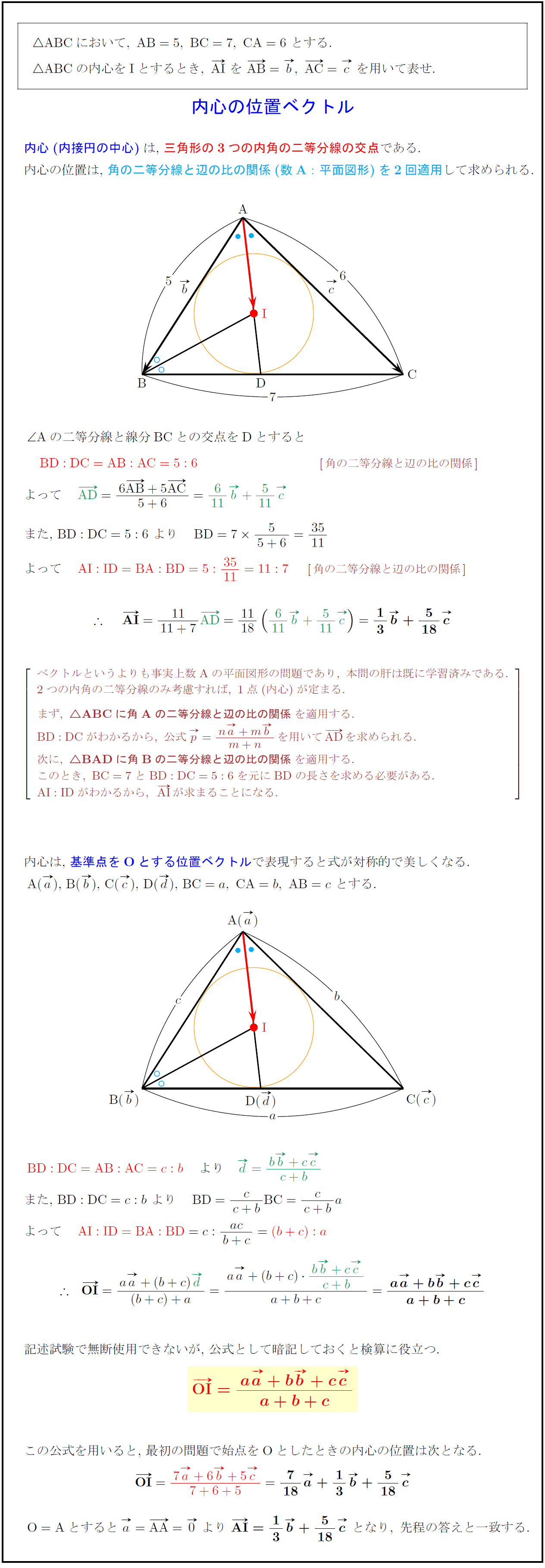


高校数学b 三角形の内心の位置ベクトル 受験の月



Wbj2mn3j6fcilm



内分点 外分点の公式と証明 高校数学の美しい物語


アンテナの設置場所


数学内分点と外分点の質問 問 次の2点abに対して 線分abを4 Yahoo 知恵袋
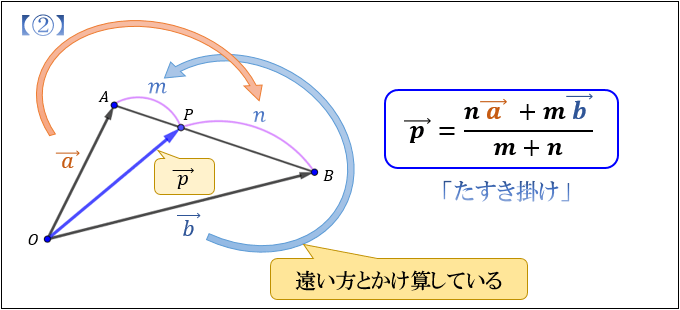


位置ベクトルの意味と内分点 外分点の位置ベクトルの考え方 アタリマエ



Wbj2mn3j6fcilm



Wbj2mn3j6fcilm



問題の解き方の何がおかしいですか 高校数学に関する質問 勉強質問サイト



2 と 4 の問題が分かりません 外分についてよく分からないので教えて下さい Clear



内分点 外分点の位置ベクトル 数学b フリー教材開発コミュニティ Ftext



位置ベクトルを超わかりやすく解説した 内分 外分 重心 理系ラボ



内分 外分 高校数学に関する質問 勉強質問サイト


内分点外分点の座標



内分と外分の違い 数学の偏差値を上げて合格を目指す
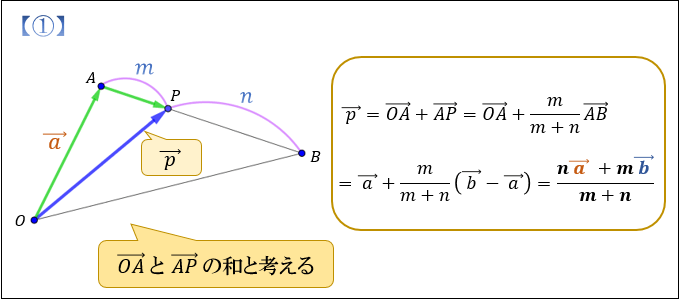


位置ベクトルの意味と内分点 外分点の位置ベクトルの考え方 アタリマエ


Studydoctor空間上の内分点 外分点の座標 数b Studydoctor



線分を内分 外分する点を書く問題は 点を書くだけじゃなくて と とか 高校 教えて Goo



アポロニウスの円の問題です Clear
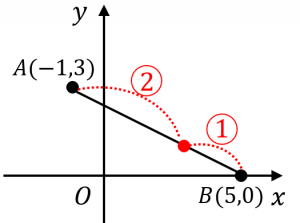


内分点と外分点の座標を求める公式 具体例で学ぶ数学



内分点 外分点の位置ベクトル 数学b フリー教材開発コミュニティ Ftext



Wbj2mn3j6fcilm



数学ii 図形と方程式 1 3 直線上の外分点の座標 Youtube



位置ベクトルとは 内分点 外分点 三角形の重心の求め方を解説 応用問題の解き方 遊ぶ数学塾
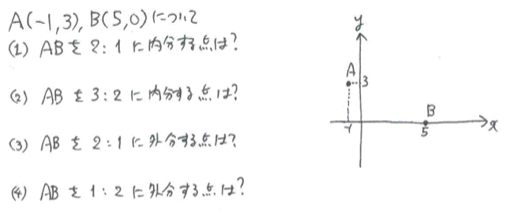


センター用プチ問題iib編



高校数学 分点公式 映像授業のtry It トライイット



高校数学a 外分とは 練習編 映像授業のtry It トライイット



桝塾 数学無料問題集 図形と式 第1講 点の座標 佐倉 練習問題 ブログ



7番の問題は公式を使う以外で解く方法はないのでしょうか 公式が難 数学 教えて Goo



Oab Ab 1 0 2 C Oc 3 I 1 D Lihat Cara Penyelesaian Di Qanda



内分点 外分点の公式と求め方 数直線 座標 ベクトル 複素数



数学a 内分 外分の点はどこにある 場所の見つけ方をサクッと解説 数スタ



高校数学 数学2 図形と方程式 単元丸ごと 問題用紙解答用紙付き 予習 復習 テスト対策 直線 円 軌跡 領域 直線 内分点 外分点 円と接線 Youtube


数学の内分点 外分点を図示する問題 外分点の求め方が全く Yahoo 知恵袋



高校数学a 線分の内分点と外分点の図示 受験の月



内分点 外分点の公式と求め方 数直線 座標 ベクトル 複素数



内分点 外分点の公式と求め方 数直線 座標 ベクトル 複素数



位置ベクトルを超わかりやすく解説した 内分 外分 重心 理系ラボ
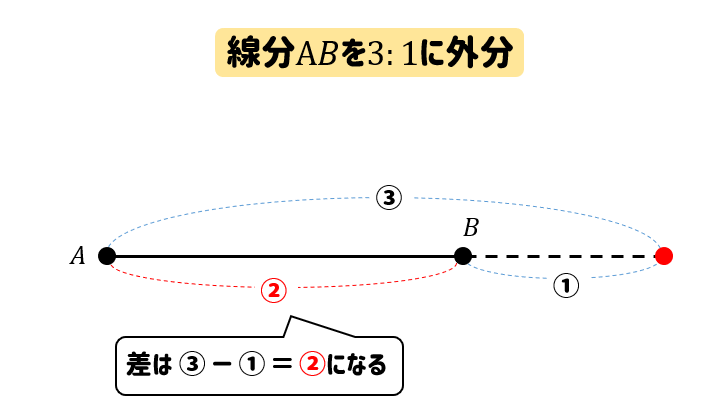


数学a 内分 外分の点はどこにある 場所の見つけ方をサクッと解説 数スタ



内分点 外分点の公式と求め方 数直線 座標 ベクトル 複素数



内分点と外分点 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



高校数学無料問題集 数b 第2章 ベクトル 位置ベクトル 桝 ます Note


分点公式 数学入試問題



基本 数直線上の内分点と外分点の座標 なかけんの数学ノート



算数 数学パズル 解答 ー 内分点 外分点の証明 ー ミスター ビーンのお気楽ブログ
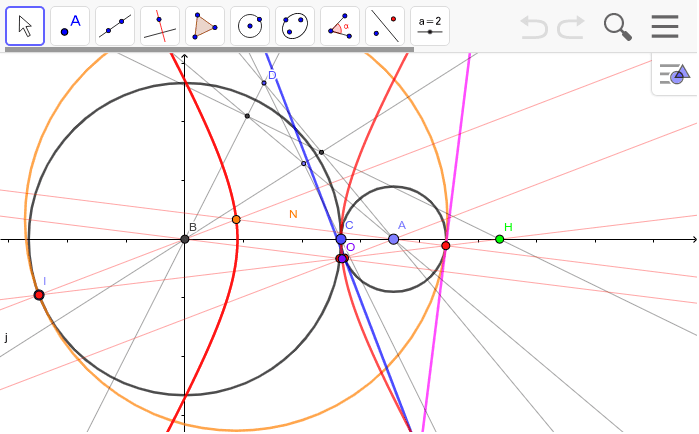


接する二円が作る楕円と双曲線 Geogebra


土地家屋調査士試験 測量士補試験で使う数学の知識 土地家屋調査士合格ブログ


内分点と外分点の求め方 思考力を鍛える数学
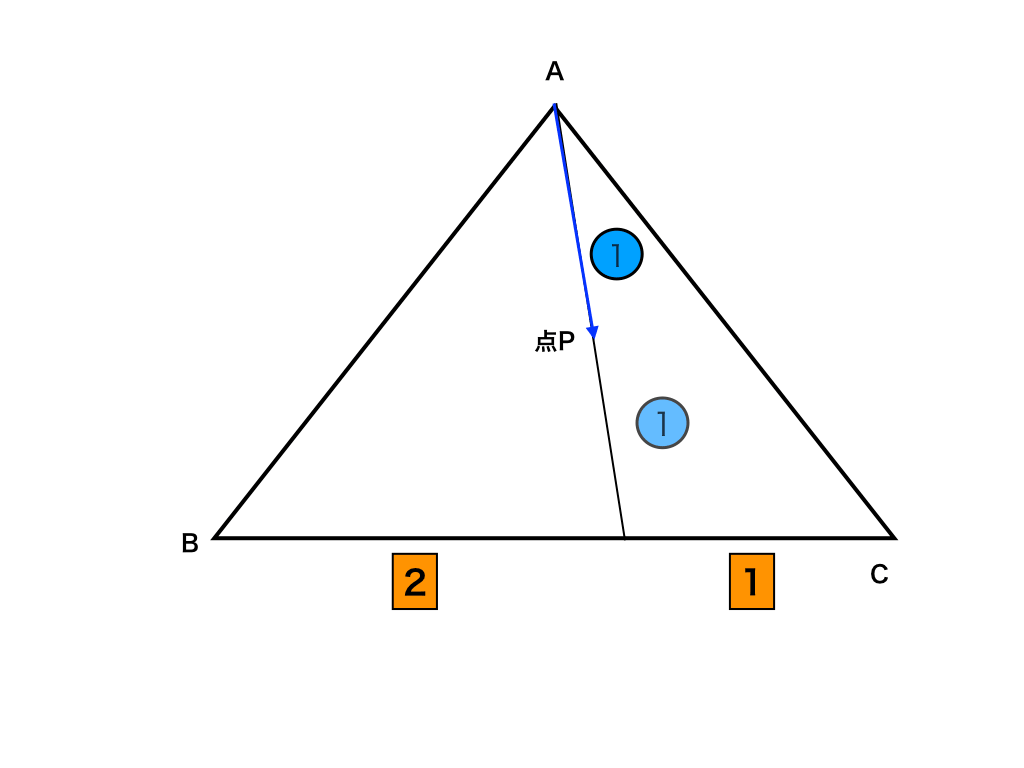


ベクトルの和で表された式から点pの位置を求める方法を解説



大学入試過去問 検索結果



直線上における内分点と外分点 数学ii By Okボーイ マナペディア



数学a 内分点と外分点の位置の求め方とコツ 教科書より詳しい高校数学


数2 内分点 外分点 No 3
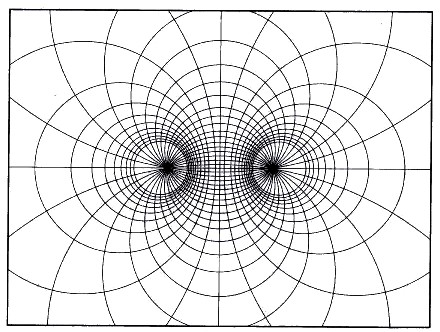


16 長さと面積 16 2 距離に関連した問題 16 2 4 アポロニウスの円 図16 5 アポロニウスの円の集合とその反転図形 宮崎 二点だけを考え 二点からの距離の和が一定である点の集合は楕円 差が一定であると双曲線です 等距離ではなく m nの距離比
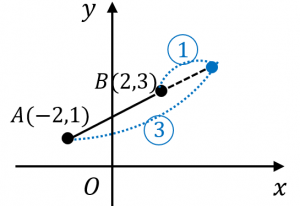


内分点と外分点の座標を求める公式 具体例で学ぶ数学



アヴニール教室



0 件のコメント:
コメントを投稿